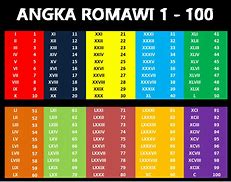
Kelas 9 Romawi

Bilangan romawi di bawah ini yang lebih besar dari D adalah ....

Correct Answer C. M

ExplanationThe correct answer is M. This is because in Roman numerals, M represents 1000, which is greater than D, which represents 500. Therefore, M is the only option that is larger than D.

Angka 24 jika ditulis dalam bilangan romawi menjadi ....

Correct Answer D. XXIV

ExplanationThe correct answer is XXIV. In Roman numerals, "X" represents 10 and "IV" represents 4. Therefore, when combined, "XXIV" represents 24.

Rumah Sinta terletak di jalan mawar nomor CXXIX . Nomor CXXIX jika diubah ke bilangan cacah menjadi ....

Correct Answer C. 129

ExplanationThe question asks for the number CXXIX to be converted to a cardinal number. CXXIX represents 129 in Roman numerals. Therefore, the correct answer is 129.

XXI , XLI , XIX , XCI , LXI Urutan bilangan romawi di atas yang tepat dari yang terkecil adalah ....

XIX , XXI , XLI , LXI , XCI

XCI, XIX , XXI , XLI , LXI

XIX , XLI, XXI , LXI , XCI

XIX , XXI , XLI , XCI, LXI

Correct Answer A. XIX , XXI , XLI , LXI , XCI

ExplanationThe given sequence is arranged in ascending order based on the Roman numerals. Starting with XIX (19), the sequence progresses to XXI (21), then XLI (41), LXI (61), and finally XCI (91). This order represents the numbers from smallest to largest.

Semua persamaan nilai angka romawi terhadap bilangan cacah berikut ini benar, kecuali ....

Correct Answer C. XCII = 82

ExplanationThe given equation XCII = 82 is incorrect because the Roman numeral XCII represents the number 92, not 82.

Bilangan romawi di bawah ini yang bernilai paling besar adalah ....

Correct Answer D. CIV

ExplanationThe Roman numeral "CIV" represents the number 104. Among the given options, "CIV" has the highest numerical value. "VIII" represents 8, "XIII" represents 13, and "LIV" represents 54, all of which are smaller than 104. Therefore, "CIV" is the Roman numeral with the highest value among the given options.

– 28 = N . Nilai N jika ditulis dalam bilangan romawi adalah .....

Correct Answer C. LXXII

ExplanationThe equation 100 - 28 = N can be simplified to 72 = N. The Roman numeral representation of 72 is LXXII.

XL merupakan bilangan romawi yang bernilai ....

Correct Answer D. 40

ExplanationXL merupakan bilangan romawi yang bernilai 40.

Bilangan X pada bilangan romawi jika dijadikan bilangan cacah sama dengan ....

Correct Answer B. 10

ExplanationThe question is asking for the Arabic numeral equivalent of the Roman numeral X. In Roman numerals, X represents the number 10.

MM : XX + XXIII = .... Hasil dari operasi hitung campuran di atas adalah ....

Correct Answer D. CXXIII

ExplanationThe given equation is XX + XXIII. XX represents the number 20 and XXIII represents the number 23 in Roman numerals. When we add these two numbers, we get 20 + 23 = 43. In Roman numerals, 43 is represented as XLIII. Therefore, the correct answer is CXXIII.

0%0% found this document useful, Mark this document as useful

0%0% found this document not useful, Mark this document as not useful

%PDF-1.4 %Çì�¢ 5 0 obj <> stream xœlÝM¯%×yžáyÿŠJï÷sUMdâ22 dYV" ° ?ûP¤ìœ«`@‚Êlru«©[Úµ®ýüË÷×G|}þß/ÿü»Ÿ¾ýí?œïø·oÿòíó_OÌýýäìÇÞßÿõ÷ßÿû÷?{}äûáëc^ûþÇ¬ùþ¯ø6¯Ó¯ü^g>:óûOßzó|¼êû5¯¸çûŸ¾õä~¼îï{ïGÝñùäžëc÷ý—É�ûz?øú§ùÓ·úù¯÷>ÝÇžëó¯wíç_ïóÏúùç¸_çzÿsÏy}\ïXñ±ï³þü#7ûýc~þq9g}Äû�¯í�3¿ü°úúÃNþ¯®Ï_˜ëú�?ð×Ãÿô×#tíÇ5ŸgýõIÄýþ+ßŸ?Ÿ8ûþ)×¹?âäÏ?ÃÿÿÏóù3ŒïøÖ�ï_Šëûç¯õ¼¦ï_ÀyÝï_ã_Ÿ¼ÏÚù>zæÇuÿû¿î×û§ñýwßþúäzÿˆüþëŸ`æýúû¯…_þåû¯¾>Þ¿,¿þÿózmþú£ý—ÿþ§ÿåÉ_ðË�ÿë¿ü~÷þ©ýË·øù÷×÷_þéw?}ÿO?|û›×Çëýïò¿{ÿn»>ÿ_?|þ"üü‡}Ï|ÿâ½OÝ¯�þüëþðÓ·_þèÿûíüæûûmöÇ=¿ùýŸÿñ�ÿøÇÿýÛ¿‰ëý“Îû7?þùûßýøo?ýøç?~ÿ¯úñŸÿõÇ?üøýßÿËïÿí÷ÿüãÿùñÏ¿ýŸ?üÝ·ÿüÃ·¿ÿ£Îç¿¹ïßcŸÿøóïáç³þí?ÄëË»ÏÇýþ¢®÷/Ôù<áoþøÛþ×_þÔŸÿfþúá¯¿Eîëúü ~^ï_Ûýå·Ùß¿ÿ‚ï¿¿ÞÎ÷ûãÎÏßh?ýåÉûï¯÷oœ+¯øù÷Ð_ž¼ÿ6Œ�é_Ÿ¼”O~ýóüéÛçß©Ÿ?Ï«>ÿÞ¹þ{õ¼¶Ÿ¿•ßðÏ?öûçÿ½ÿ®þ§¿<º¿üë=÷ç£žú�«ÏÏó?<œënþÈé¾%n~øûYÿÈ×ûïË¯k+øáïßl_ÿÈ|ÿ}ø~ÊÃ¸òÅŸ3jäþ,ßÿ1Ç~øUûË/åÿ÷«{½^>úúïÉûQú¨|Ô>�Ž�.yúðôáéÃÓ‡§Ož><}xúðôáéÓÓ§§OOŸž>=}zúôôééÓÓ§§/O_ž¾<}yúòôåéËÓ—§/O_ž¾=}{úöôíéÛÓ·§oOßž¾=}{úñôü'é~þ÷yúñôãéÇÓ�§O?ž~=ýzúõôëé×Ó¯§_O¿ž~=ýzúãé�§?žþxúãé�§?žþxúãé�§¿<ýåé/OyúËÓ_žþòô—§¿<ýåéoO{úÛÓßžþöô·§¿=ýíéoOoko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ´ö¼híûÑ×ÓŸ}?úzú÷£¯§?úzú÷£¯§?úzú÷£¯§?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�<=}?òô´ö¼híû‘§§µŸŸ¢ûÈÓÓÚ÷#OOkß�<=}?òô´öýÈÓÓÚ÷#OOkß�8}ØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ† [¶6lmØÚ°µakÃÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶Ö›/[~j]~j]~j]~j]~j]E?µ.?µ.?µ.?µ.êþ~äéýÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔº|CÜ¾!nß·oˆÛ7Äíâö qû†¸}CÜ¾!nß·oˆÛ7Äíâö qû†¸}CÜ¾!nß·oˆÛ7Äíâö qû†¸}CÜ¾!nß·oˆÛ7Äíâö qû†¸}CÜ¾!nß·oˆÛ7Äíâö qû†¸}CÜ¾!nß·oˆÛ7Äíâö qÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖúí#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xÃÖÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅûÀŠÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikÓÖ¦M[›¶6mmÚÚ´µikËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙZ¿PcdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+~?òôÞÆ’�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xžX±½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙÚËÖ^¶ö²µ—½líek/[{ÙZ¿=£5Ä!n qkˆ[CÜâÖ·†¸5Ä!n qkˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†øçà‘§·µâÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†xqÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–-[[¶¶lmÙÚ²µekËÖ–m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[ë·g´¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ¬ø²µ—½líek/[{ÙÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¶ö¶µ·½mímko[{ÛÚ‡/Ô�·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–wXwYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â–·¬¸eÅ-+nYqËŠ[VÜ²â~`ÅmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖ¶m[Û¶¶mmÛÚ¶µmkÛÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶ÖoÏ( qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4ÄïGžÞÖÞ¶ö¶µ·½mímko[{ÛÚÛÖÞ¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzÑÚ÷#Oïm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm,¿=£dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+~?òô¶VV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²âz`ÅckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µckÇÖŽ[;¶vlíØÚ±µkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vmíÚÚµµkk×Ö®][»¶vm_¨‘²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠ

Kelas 4-5 Bilangan Romawi

Bab 5 Algoritma dan Pemrograman (Dekomposisi menggunakan bahasa pemrograman C++) - Informatika SMP/MTs Kelas 9Read less

Kelas 9 Romawi

Bilangan romawi di bawah ini yang lebih besar dari D adalah ....

Angka 24 jika ditulis dalam bilangan romawi menjadi ....

Rumah Sinta terletak di jalan mawar nomor CXXIX . Nomor CXXIX jika diubah ke bilangan cacah menjadi ....

XXI , XLI , XIX , XCI , LXI Urutan bilangan romawi di atas yang tepat dari yang terkecil adalah ....

Semua persamaan nilai angka romawi terhadap bilangan cacah berikut ini benar, kecuali ....

Bilangan romawi di bawah ini yang bernilai paling besar adalah ....

– 28 = N . Nilai N jika ditulis dalam bilangan romawi adalah .....

XL merupakan bilangan romawi yang bernilai ....

Bilangan X pada bilangan romawi jika dijadikan bilangan cacah sama dengan ....

MM : XX + XXIII = .... Hasil dari operasi hitung campuran di atas adalah ....

Bài tương tự

Rumah Cahaya Untukmu

Slot Bet Kecil Menang Besar

Permainan Baru Slot Domino Terbaru 2024 Gratis

Baju Kuning Hijab Warna Apa